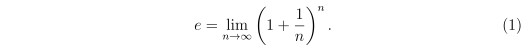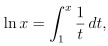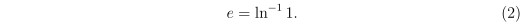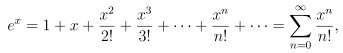昌小澤的秘密基地

下了組長之後 除了上課和處理協行的事情之外
大部分的時間都待在教師辦公室
中山是同一科老師的辦公室會在一起
所以有了很多時間可以跟其他的老師討論 有時光聽老師們討論也就可以學到很多東西
對應到教學上的改變就是 處理某些內容時會變得比較細膩

分享一下

利用中午吃飯時間做的

上次教高二教到兩面角的時候
為了讓學生能了解我們在計算正四面體的兩面角時 黑板上所畫的那些線到底是在哪裡
當時做了一個正四面體的模型(詳見[無名] 今天的回家作業)
當時還被高三的老師借去用 因為模擬考出了一題跟正四面體有關的難題
只是學期末時已經被我弄得爛爛的 所以就沒有留下來

這學期我做了一個嘗試
想要把數學有趣的一面 生活化的一面 介紹給學生
於是就利用每週一節的「書報閱讀」課來進行

其實我在平常的課堂上 就會去講一些這方面的東西

雖然最近忙到都沒有時間寫網誌
但植樹節談「質數」的活動不能就這樣結束
幸運的是 (對我來說啦)
從去年植樹節後到今年 都沒有新的「梅仙涅質數 (Mersenne prime)」再被找出
所以 今年的植樹節談「質數」就到這裡結束啦 謝謝大家 XD

上一篇 我們介紹了三種自然底數 (或稱為尤拉常數) e 的定義
但如果一開始不說
其實還蠻難想像從這樣三個完全不同方向所得到的值 竟然會是一樣的
因此 接下來我要談的是
「這三種完全迥異的定義方式所定義出來的 e, 我們是怎麼肯定他們是 "相同" 的」

上周和 S 閒聊時 無意間聊到自然底數 e (又稱尤拉常數)
就我們從高中第一次接觸到他 一直到念了大學 大致上看到的定義有下面三種:
1. 定義下面數列的極限值為 e:

2. 我們先定義對數函數

則自然對數 ln x 的底數, 我們就定義為 e. 即

今年數學的指考題目 可以說是兩樣情
數甲維持一慣出題風格
沒有繁瑣的計算 觀念清楚就很容易作答
難度也維持跟之前幾年的差不多
所以一般普遍認為 今年的五標應該跟去年差不多

這個問題困擾我很久:
"若 x + 2 = 4, 則 x = 2 或 x = 3" 這樣的敘述是否正確?
會這樣想的原因是 "或" 在邏輯上的意思不就是 "只要有一個是正確的 整個敘述就會是對的"
因此 上面的敘述看起來應該是對的
但我們都知道 在考試時這樣作答是錯誤的!

雖然因為當兵而錯過了 3 月 12 日
但本部落格一年一度慶祝「植樹節」的活動並不會因此而暫停
沒錯!! 我們又要來關心是否有新的「梅仙涅質數 (Mersenne prime)」再被找出
而今年恰逢本活動的第五週年 所以先來個特別企劃
讓我們先來認識一下 到底什麼是梅仙涅質數

故事發生在去年 12 月初借住台南 S 學弟家
同樣是高中數學教師的 S 房裡有許多跟數學有關的書籍與資料
其中有一堆是從他退休的師父那邊搬回來的
而我 就在那堆快接近 "古董" 的書堆理尋找有趣的東西
翻著翻著 翻出一本歷屆大學聯考數學科考題 從民國 6x 年到 8x 年

最近迷上噗浪 卯起來噗
因為可以想到什麼就寫什麼 不用管完不完整 看不看得懂
而且在噗浪裡寫一個噗與在部落格寫一篇網誌的時間 真的是差太多了
有噗浪的朋友一起來噗吧 ^^

今年的大學入學指定科目考試 (即一般所稱的「指考」) 可以說是萬眾注目
一來 是有新朋友「公民與社會」科的加入
二來 這是實施高中 95 暫綱後的第一次指考 受注目的程度可想而知
在數學科的部分
根據 97 年 9 月 30 日所公告的「數學考科說明」中

這次高等幾何的期末考, 考了一個跟圓切線有關的作圖問題:
「給定一圓 作圓外一點對此圓的切線 以及 圓上一點對此圓的切線」.
特別的是, 他只能利用直尺而不能使用圓規.
下面我把尺規作圖以及只能用尺的作圖方法整理出來.

之前教高二排列組合時 有兩個地方當時我覺得教的很不好
一個是「環狀排列」 另一個就是「分組分堆」
不好講的地方在於 到底時麼時候要乘 n 階層 什麼時候要除 n 階層
或甚至 為什麼這裡要乘 n 階層 這裡卻要除 n 階層
有時候 連我自己都會搞不清楚狀況 還蠻糟糕的 >

這是剛剛在聊天時 學弟說的 XD

問：一個銅板擲出正面的機率是多少？

答：1/2。

上離散的時候 老師給的
乍看之下很花 其實他們的字首與字尾是有規律的
字尾的部分 多邊形就是 -agon 多面體就是 -ahedron
前面的數字就是字首 兩邊都一樣
但討厭的是 都不是我們平常會看到的字 XP

這是有一天去找實習的指導老師聊天時 聊著聊著聊到了教甄
他給了我這個問題 要我試試看
想來想去我只想得到用微積分的方法 但老師說用高中方法他至少有兩種方式可以做
所以在 MSN 遇到服替代役中的強者學弟時 就順便問了一下
結果 問出了很多方法 有些還蠻有趣的 ^^

某廠商委託民調機構在甲、乙兩地調查聽過某項產品的居民佔當地居民之百分比 (以下簡稱為「知名度」)。結果如下：在 95% 信心水準之下，該產品在甲、乙兩地的知名度之信賴區間分別為 [ 0.50 , 0.58 ] 、 [ 0.08 , 0.16 ] 。試問下列哪些選項是正確的？
(1) 甲地本次的參訪者中， 54% 的人聽過該產品
(2) 此次民調在乙地的參訪人數少於在甲地的參訪人數
(3) 此次調查結果可解讀為：甲地全體居民中有一半以上的人聽過該產品的機率大於 95%
(4) 若在乙地以同樣方式進行多次民調，所得知名度有 95% 的機會落在區間 [ 0.08 , 0.16 ]

又到了一年一度的植樹節
不免俗的 我們還是要來看一下去年一整年在梅仙涅質數 (Mersenne prime) 的搜尋上 是否有新的進展

在經過去年很不幸的空手而回後 今年的結果可以說是讓人們大為振奮
因為一次出現了兩個新的梅仙涅質數