close
故事發生在去年 12 月初借住台南 S 學弟家
同樣是高中數學教師的 S 房裡有許多跟數學有關的書籍與資料
其中有一堆是從他退休的師父那邊搬回來的
而我 就在那堆快接近 "古董" 的書堆理尋找有趣的東西
翻著翻著 翻出一本歷屆大學聯考數學科考題 從民國 6x 年到 8x 年
(當時我還只是個可愛的小學生 XD)
我們兩個就一邊看著以往的聯考題 一邊見證著這 30 幾年來高中數學內容與考試方式的變遷
順便驚嘆那些現在我們覺得是基本題的問題 原來是當時某年聯考的新題目
現在學生真的是辛苦 (老師也是 要教這麼難的東西)
無意間翻到這一題: 66 年社會組的多選題
3^(2n+1) + 5^(2n-1) 恆被 k 整除
試利用數學歸納法找出整數 k 之值為 (1) 2 (2) 4 (3) 8 (4) 16 (5) 32
我看到這個題目的第一的想法是 這個題目會不會太狠了 ><
怎麼說呢? 真的做一次你就會知道了
當 n = 1 時: 3^3 + 5^1 = 32 => 這是 32 的倍數
所以答案是 (1)(2)(3)(4)(5)? 不用想也知道沒有這麼便宜的事
當 n = 2 時: 3^5 + 5^3 = 368 => 這不是 32 的倍數 但是 16 的倍數
所以答案是 (1)(2)(3)(4)?
有沒有可能代 n = 3 時 就變成只剩下 8 的倍數?
當 n = 3 時: 3^7 + 5^5 = 5312 => 還好他還是 16 的倍數
但真的之後都會是 16 的倍數嗎?
會不會在某個地方又降到只剩下 8 的倍數?
想到這裡 我開始喜歡上這個題目
因為他跟課本裡所給的相關例題 有著很大的不同
一來 課本的例題通常在代到 n = 2 時 (慘一點的在代 n = 1 時 答案就是該質數)
你會發現他是某一個 "質數" 的倍數 答案當然就是這個質數
(如果說這一群數字都只能被 1 整除 這問題會不會就太好笑了點)
但這一題 除非找到某個 n 代入後 他只會是 2 的倍數 而不是 4, 8, 16, 32 的倍數
不然上面的問題就會一值 "困擾" 著我們
這不就是 "猜想" 與 "證明" 存在於數學界的目的?
這不就是在使用 "數學歸納法" 時該有的精神?
就是因為猜不透 所以才要用證明來確定他的正確性
就是因為不可能把所有正整數一個個代進來檢驗 所以才要靠數學歸納法把所有骨牌推倒
回到原本的問題
我們就先猜他們會是 16 的倍數 然後利用數學歸納法來證明看看
証法如下:

這是念頭一轉
如果無法順利證明出來他是 16 的倍數
那我是不是就得再假設他是 8 的倍數 再做一次數學歸納法?
(運氣不好的話 還得再用 4 做第三次的數學歸納法)
哪來的那麼多時間?
這時 S 學弟跟我說
他印象中 這類找倍數的問題 是可以用 "二項式定理" 來處理的
而且 一次就可以得到答案 不用在那邊猜來猜去
我們兩個花了點時間 把他給做了出來 (還真不好湊這些數字)
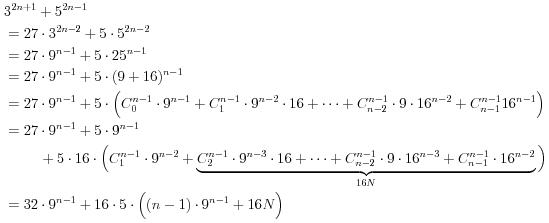
原來二項式定理是個這麼強的定理 我從來沒有想過可以這樣使用它
但隔了幾天後我回頭過來重看這個問題
當看到整個式子的最後一行時 突然想到
我使用 "二項式定理" 的目的 是為了處理上面的連考題 而不是只是單純證明他是 16 的倍數
也就是說 在做題目的時候 我根本不知道他是 16 的倍數
而在這樣的狀況下 前面有個 32 x 9^{n-1}
所以除非我能說 "16 x 5 x 一堆組合數的和" 就只是 16 的倍數
(也就是那一堆組合數的和必須得是奇數)
不然 整個式子還是有可能是 32 的倍數!!!
(註: 實際上 當時我和 S 只有做到倒數第二行就停手 因為那裡就能得到他是 16 的倍數)
而最後那一行 是為了方便我這篇網誌能繼續寫下去而加進去的
所以請大家先把那一行蓋起來 ^^|||)
想了很久 我想不到要怎麼說那堆東西會是奇數
直到過了三個禮拜後再次借住在 S 家 我把這個困擾告訴了他
然後 兩個人又弄了一陣子 直到寫出 16 x 5 x [(n - 1) x 9 + 16N] 才找到答案
很明顯的 只要 n 是偶數 (也就是 n - 1 是奇數) 時 這個數就只能是 16 的倍數
當然 當 n 是奇數 (也就是 n - 1 不是奇數) 時 加號前後都會是 32 的倍數
但別忘了 這是對 "所有的正整數 n" 都要成立
所以沒有關係 他是 32 的倍數就一定會是 16 的倍數
因此對所有的正整數 n, 3^(2n+1) + 5^(2n-1) 恆為 16 的倍數 Q.E.D.
得到這樣的結論 我感到非常的開心
一來 真的不用先猜就可以直接把答案給找出來 (而這個做法也就是證明的方法)
二來 這組數字的特性也被展現了出來
當成數列來看 奇數項是 32 的倍數 偶數項則是 16 的倍數
三來 我在猜 這類猜倍數的問題 會不會就是先經過這樣的計算
確定答案是誰後 再轉變成數學歸納法的問題
不然哪有人這麼有時間 去發現這樣的指數相加後 剛好都會是某個數倍數
(可以試試看 隨便出個問題自己玩玩 應該很容易就變成只有 1 這個公因數
不過 我沒有實際這樣玩過就是了 ^^|||)
所以 如果我希望這個數列的前兩項是 32 的倍數 到第三項才變成 16 的倍數
要怎麼來反湊這個題目呢?
科科...
P.s. 這篇網誌寫了一個月終於寫成了 只是新年的第一篇就是數學 會不會嚇跑太多人啊 XD
同樣是高中數學教師的 S 房裡有許多跟數學有關的書籍與資料
其中有一堆是從他退休的師父那邊搬回來的
而我 就在那堆快接近 "古董" 的書堆理尋找有趣的東西
翻著翻著 翻出一本歷屆大學聯考數學科考題 從民國 6x 年到 8x 年
(當時我還只是個可愛的小學生 XD)
我們兩個就一邊看著以往的聯考題 一邊見證著這 30 幾年來高中數學內容與考試方式的變遷
順便驚嘆那些現在我們覺得是基本題的問題 原來是當時某年聯考的新題目
現在學生真的是辛苦 (老師也是 要教這麼難的東西)
無意間翻到這一題: 66 年社會組的多選題
3^(2n+1) + 5^(2n-1) 恆被 k 整除
試利用數學歸納法找出整數 k 之值為 (1) 2 (2) 4 (3) 8 (4) 16 (5) 32
我看到這個題目的第一的想法是 這個題目會不會太狠了 ><
怎麼說呢? 真的做一次你就會知道了
當 n = 1 時: 3^3 + 5^1 = 32 => 這是 32 的倍數
所以答案是 (1)(2)(3)(4)(5)? 不用想也知道沒有這麼便宜的事
當 n = 2 時: 3^5 + 5^3 = 368 => 這不是 32 的倍數 但是 16 的倍數
所以答案是 (1)(2)(3)(4)?
有沒有可能代 n = 3 時 就變成只剩下 8 的倍數?
當 n = 3 時: 3^7 + 5^5 = 5312 => 還好他還是 16 的倍數
但真的之後都會是 16 的倍數嗎?
會不會在某個地方又降到只剩下 8 的倍數?
想到這裡 我開始喜歡上這個題目
因為他跟課本裡所給的相關例題 有著很大的不同
一來 課本的例題通常在代到 n = 2 時 (慘一點的在代 n = 1 時 答案就是該質數)
你會發現他是某一個 "質數" 的倍數 答案當然就是這個質數
(如果說這一群數字都只能被 1 整除 這問題會不會就太好笑了點)
但這一題 除非找到某個 n 代入後 他只會是 2 的倍數 而不是 4, 8, 16, 32 的倍數
不然上面的問題就會一值 "困擾" 著我們
這不就是 "猜想" 與 "證明" 存在於數學界的目的?
這不就是在使用 "數學歸納法" 時該有的精神?
就是因為猜不透 所以才要用證明來確定他的正確性
就是因為不可能把所有正整數一個個代進來檢驗 所以才要靠數學歸納法把所有骨牌推倒
回到原本的問題
我們就先猜他們會是 16 的倍數 然後利用數學歸納法來證明看看
証法如下:

這是念頭一轉
如果無法順利證明出來他是 16 的倍數
那我是不是就得再假設他是 8 的倍數 再做一次數學歸納法?
(運氣不好的話 還得再用 4 做第三次的數學歸納法)
哪來的那麼多時間?
這時 S 學弟跟我說
他印象中 這類找倍數的問題 是可以用 "二項式定理" 來處理的
而且 一次就可以得到答案 不用在那邊猜來猜去
我們兩個花了點時間 把他給做了出來 (還真不好湊這些數字)
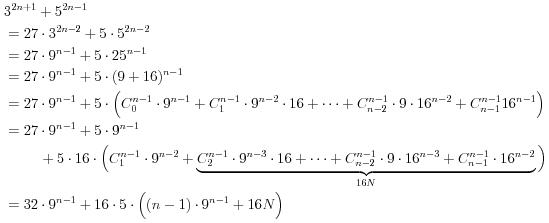
原來二項式定理是個這麼強的定理 我從來沒有想過可以這樣使用它
但隔了幾天後我回頭過來重看這個問題
當看到整個式子的最後一行時 突然想到
我使用 "二項式定理" 的目的 是為了處理上面的連考題 而不是只是單純證明他是 16 的倍數
也就是說 在做題目的時候 我根本不知道他是 16 的倍數
而在這樣的狀況下 前面有個 32 x 9^{n-1}
所以除非我能說 "16 x 5 x 一堆組合數的和" 就只是 16 的倍數
(也就是那一堆組合數的和必須得是奇數)
不然 整個式子還是有可能是 32 的倍數!!!
(註: 實際上 當時我和 S 只有做到倒數第二行就停手 因為那裡就能得到他是 16 的倍數)
而最後那一行 是為了方便我這篇網誌能繼續寫下去而加進去的
所以請大家先把那一行蓋起來 ^^|||)
想了很久 我想不到要怎麼說那堆東西會是奇數
直到過了三個禮拜後再次借住在 S 家 我把這個困擾告訴了他
然後 兩個人又弄了一陣子 直到寫出 16 x 5 x [(n - 1) x 9 + 16N] 才找到答案
很明顯的 只要 n 是偶數 (也就是 n - 1 是奇數) 時 這個數就只能是 16 的倍數
當然 當 n 是奇數 (也就是 n - 1 不是奇數) 時 加號前後都會是 32 的倍數
但別忘了 這是對 "所有的正整數 n" 都要成立
所以沒有關係 他是 32 的倍數就一定會是 16 的倍數
因此對所有的正整數 n, 3^(2n+1) + 5^(2n-1) 恆為 16 的倍數 Q.E.D.
得到這樣的結論 我感到非常的開心
一來 真的不用先猜就可以直接把答案給找出來 (而這個做法也就是證明的方法)
二來 這組數字的特性也被展現了出來
當成數列來看 奇數項是 32 的倍數 偶數項則是 16 的倍數
三來 我在猜 這類猜倍數的問題 會不會就是先經過這樣的計算
確定答案是誰後 再轉變成數學歸納法的問題
不然哪有人這麼有時間 去發現這樣的指數相加後 剛好都會是某個數倍數
(可以試試看 隨便出個問題自己玩玩 應該很容易就變成只有 1 這個公因數
不過 我沒有實際這樣玩過就是了 ^^|||)
所以 如果我希望這個數列的前兩項是 32 的倍數 到第三項才變成 16 的倍數
要怎麼來反湊這個題目呢?
科科...
P.s. 這篇網誌寫了一個月終於寫成了 只是新年的第一篇就是數學 會不會嚇跑太多人啊 XD
全站熱搜


 留言列表
留言列表


