上一篇 我們介紹了三種自然底數 (或稱為尤拉常數) e 的定義
但如果一開始不說
其實還蠻難想像從這樣三個完全不同方向所得到的值 竟然會是一樣的
因此 接下來我要談的是
「這三種完全迥異的定義方式所定義出來的 e, 我們是怎麼肯定他們是 "相同" 的」
其實它的證明 在微積分課本裡 就只是定理後面的例題或作業 其實並不難
只是 微積分是以式 (2) 當作自然底數 e 的定義
因此會看到的是式 (1) 與式 (3) 的值剛好皆為 e 的證明
但我覺得 如果只有這樣 會讓人覺得式 (1) 與式 (3) 的結果是依附在式 (2) 這個定義之下
所以 在後面我會花點力氣來說說 如何從式 (1) 或式 (3) 出發來得到另外兩個
還有一件事情要寫在前面
就是下面的證明過程中 其實會用到不少微積分 (或高等微積分) 裡的定理
在為了保持可讀性與易讀性的原則下
請原諒我 "忽略" 介紹他們 並且直接使用該定理
或者用比較 "直覺" 的方式來解釋他們
現在 我們以式 (2) 為自然底數 e 的定義
開始來解釋式 (1) 的極限值真的是由式 (2) 所定義出來的 e
我們要考慮的是下面數列的極限
而是要藉由知道 {ln (a_n)} 的極限值後 反推而得
過程如下:
因為 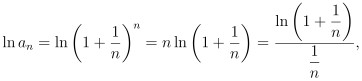
故根據羅必達法則可以得到 {ln (a_n)} 的極限值為 1:
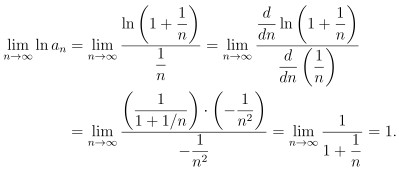
又自然底數 e 的定義是 e = ln-1 1
也就是說 若 ln x = 1, 則 x 的值就是 e
因此可由 {ln (a_n)} 的極限值為 1 得知 {a_n} 的極限為 e
(或這樣想 因為 {a_n} 的極限為 e 所以才能使 {ln (a_n)} 的極限值為 1)
Q.E.D.
要說明式 (3) 中無窮級數和的值為 e 其實很簡單
就只是對指數函數 ex 做泰勒展開式後 代 x = 1 即可得到
唯一的問題就只是 如何由式 (2) 的定義得到 ex 的導數
其方法我在上一篇有提到 這裡再做一遍: 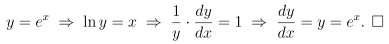
有了 ex 的導數還是 ex 的結論後 剩下的 就只是去套泰勒展開式罷了:
考慮 f(x) = ex 在 x = 0 處的泰勒展開式 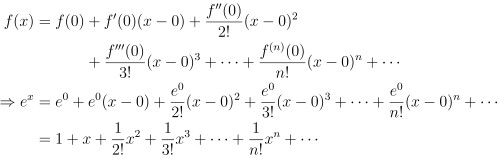
因為這個幂級數的收斂範圍為整個實數
因此可以令 x = 1 代入而得到式 (3)
(不過 說實在的 上面的做法與其說 "得到這個無窮級數的值為 e"
不如應該說 是 "e 藉由泰勒展開式可化為這個無窮級數" 還比較貼切 ^^|||)
以上是微積分課本的觀點 (以式 (2) 為自然底數 e 的定義)
下面我們要以另外兩個式子分別當作 e 的定義 來說明他們互相還是相同的
只是不論是以式 (1) 還是以式 (3) 當作 e 的定義
要注意的事情是 此時對數函數 ln x 的底數 "不見得" 是這樣定義出來的 e !!
也就是說 我們想要去證明的就是以 e 為底的對數函數 loge x = ln x
那要怎麼證明這件事?
因為我們對 ln x 的定義是 (請見上一篇)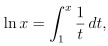
ln x 的導函數是 1/x
所以 如果我們能得到 loge x 的導函數也是 1/x
這也就表示 loge x 和 ln x 是兩個相同的對數函數
(其實還差一個常數 但只要代值進去看 就會發現這個常數為 0)
也因此對數函數 ln x 的底數的確是由式 (1) 或式 (3) 所定義出來的 e
所以 下面在證明式 (2) 的時候 我們就是用這樣的方式來看
現在我們就以式 (1) 當作 e 的定義 來證明 loge x 的導函數也是 1/x
其實就是利用導函數最原始的定義來做就行了:
令 f(x) = loge x, 所以 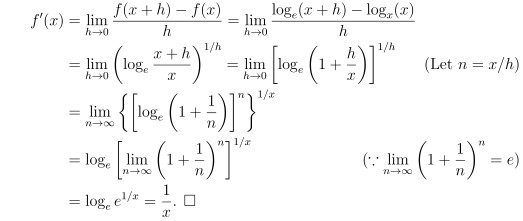
要以式 (3) 為 e 的定義來得到式 (2) 的結果
無法像上面直接用導函數的定義
所使用的方法是先找到 ex 的導函數 再去找 loge x 的導函數
令 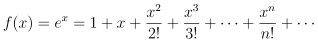
所以 ex 的導函數為
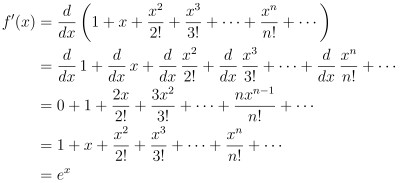
故根據隱函數微分法 可以得到 loge x 的導函數為 1/x:
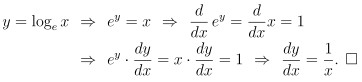
那式 (3) 和式 (1) 怎麼互通呢? 這是高等微積分裡一個很重要的定理:
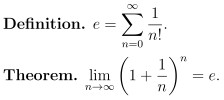
(Principles of Mathematical Analysis, 3th, Walter Rudin)
我們來看看這個證明: (下面的證明有一點瑕疵 這個後面再來解釋)
我們考慮下面兩個數列 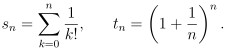
我們對 tn 做二項式展開 得到
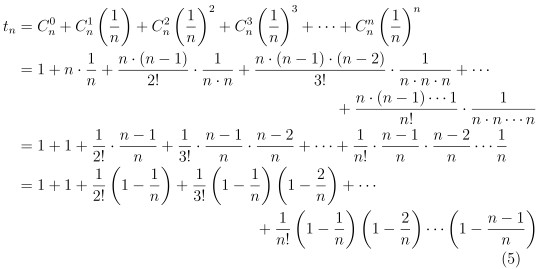
接著拿 tn 與 sn 的每一項做比較 可以簡單得到
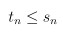
因此 兩邊同時對 n 取極限 可以得到
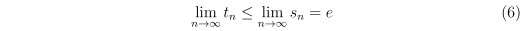
On the other hand, 我們先選定隨意的一個數 m
故當 n 取得比 m 大時 由式 (5) 可以推得 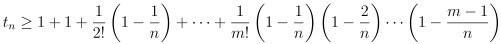
(即右半邊只加到第 m 項就對了)
故兩邊同時對 n 取極限 (m 我們固定不動) 就會有 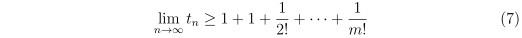
注意到右半邊剛好是 sm
即 "數列 {tn} 的極限比 {sm} 裡的「每一項」都還要大 (因為 m 是隨意選的一個數)"
因此 即使我們對 {sm} 取極限 其極限還是會比 {tn} 的極限小
所以我們得到 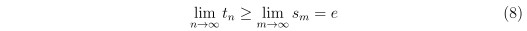
合併式 (6) 與式 (8) 的結果 就會得到
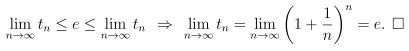
簡單講一下上面證明的瑕疵
但因為會用到高等微積分的東西 所以如果沒有想要深入追究的話 這一段是可以跳過的
上面證明有一個很嚴重的問題 在式 (6) 和式 (7) 的地方
以式 (6) 來說 因為 {tn} 每一項都比 {sn} 小 所以我們說 {tn} 的極限比 {sn} 小
但一個重要的問題是 如果 {tn} 本身不收斂 就完全沒有式 (6) 的關係了!!
所以 正確的說法應該是 limsup tn 而不是 lim tn
同樣的理由 式 (7) 應該要改為 liminf tn 才是正確的
因此 最後得到的是 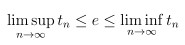
而因為一個數列的 limsup 和 liminf 指向同一個值
根據兩者的定義 我可以同時得到 "數列 {tn} 收斂" 而且 "其極限值為共同值 e"
至於 什麼是 limsup 跟 liminf ?
這就容我不在這裡多說了 要不然會寫不完啊~~~
後記:
從開始想寫這一篇文章 到 今天真的寫完 花了將近 1 個半月
其實 上面那些證明對我來說都很容易找得到且容易看得懂
但想到要寫得讓大部份的人可以看得懂 這真的讓我傷透腦筋
此外 再寫上篇的時候 一邊寫才一邊發現
有不少東西 我只是有 "印象" 但從來沒有深究過
因此把那些資料翻出來重讀了好幾次 才敢把他寫出來
再加上工作的關係 就只能每個週末挪一點時間出來寫
這下篇就是這樣接力寫了四個星期才完成
很辛苦 但很有成就感
尤其是看到上篇一個月就將近 100 人點閱
我相信這樣的文章 對某些人是有幫助的
這樣 我就開心了 ^^
參考資料: Thomas' Calculus, 10th, Finney, Weir, Giordano
Principles of Mathematical Analysis, 3th, Walter Rudin
毛起來說 e, Eli Maor, 鄭惟厚 譯 (之前沒有注意到 一直以為鄭惟厚只翻譯統計類的書 XD)
高觀點下的初等數學 第一卷, Felix Klein, 舒湘芹 陳義章 楊欽樑 譯
e (數字常數), 維基百科
但如果一開始不說
其實還蠻難想像從這樣三個完全不同方向所得到的值 竟然會是一樣的
因此 接下來我要談的是
「這三種完全迥異的定義方式所定義出來的 e, 我們是怎麼肯定他們是 "相同" 的」
其實它的證明 在微積分課本裡 就只是定理後面的例題或作業 其實並不難
只是 微積分是以式 (2) 當作自然底數 e 的定義
因此會看到的是式 (1) 與式 (3) 的值剛好皆為 e 的證明
但我覺得 如果只有這樣 會讓人覺得式 (1) 與式 (3) 的結果是依附在式 (2) 這個定義之下
所以 在後面我會花點力氣來說說 如何從式 (1) 或式 (3) 出發來得到另外兩個
還有一件事情要寫在前面
就是下面的證明過程中 其實會用到不少微積分 (或高等微積分) 裡的定理
在為了保持可讀性與易讀性的原則下
請原諒我 "忽略" 介紹他們 並且直接使用該定理
或者用比較 "直覺" 的方式來解釋他們
現在 我們以式 (2) 為自然底數 e 的定義
開始來解釋式 (1) 的極限值真的是由式 (2) 所定義出來的 e
我們要考慮的是下面數列的極限

而是要藉由知道 {ln (a_n)} 的極限值後 反推而得
過程如下:
因為
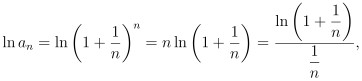
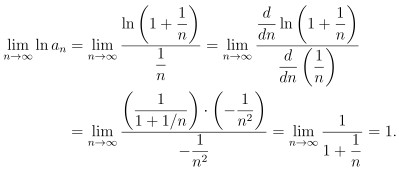
也就是說 若 ln x = 1, 則 x 的值就是 e
因此可由 {ln (a_n)} 的極限值為 1 得知 {a_n} 的極限為 e
(或這樣想 因為 {a_n} 的極限為 e 所以才能使 {ln (a_n)} 的極限值為 1)
Q.E.D.
要說明式 (3) 中無窮級數和的值為 e 其實很簡單
就只是對指數函數 ex 做泰勒展開式後 代 x = 1 即可得到
唯一的問題就只是 如何由式 (2) 的定義得到 ex 的導數
其方法我在上一篇有提到 這裡再做一遍:
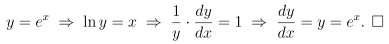
考慮 f(x) = ex 在 x = 0 處的泰勒展開式
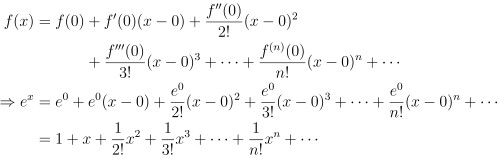
因此可以令 x = 1 代入而得到式 (3)

(不過 說實在的 上面的做法與其說 "得到這個無窮級數的值為 e"
不如應該說 是 "e 藉由泰勒展開式可化為這個無窮級數" 還比較貼切 ^^|||)
以上是微積分課本的觀點 (以式 (2) 為自然底數 e 的定義)
下面我們要以另外兩個式子分別當作 e 的定義 來說明他們互相還是相同的
只是不論是以式 (1) 還是以式 (3) 當作 e 的定義
要注意的事情是 此時對數函數 ln x 的底數 "不見得" 是這樣定義出來的 e !!
也就是說 我們想要去證明的就是
因為我們對 ln x 的定義是 (請見上一篇)
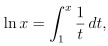
這也就表示 loge x 和 ln x 是兩個相同的對數函數
(其實還差一個常數 但只要代值進去看 就會發現這個常數為 0)
也因此對數函數 ln x 的底數的確是由式 (1) 或式 (3) 所定義出來的 e
所以 下面在證明式 (2) 的時候 我們就是用這樣的方式來看
現在我們就以式 (1) 當作 e 的定義 來證明 loge x 的導函數也是 1/x
其實就是利用導函數最原始的定義來做就行了:
令 f(x) = loge x, 所以
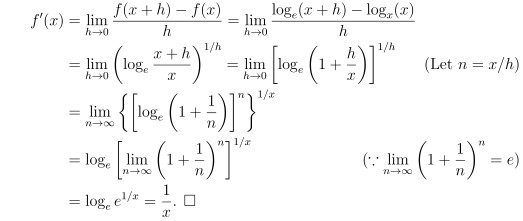
要以式 (3) 為 e 的定義來得到式 (2) 的結果
無法像上面直接用導函數的定義
所使用的方法是先找到 ex 的導函數 再去找 loge x 的導函數
令
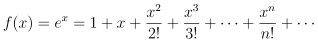
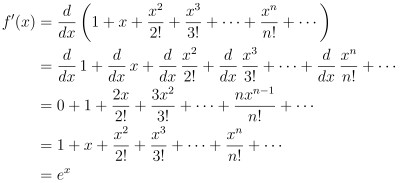
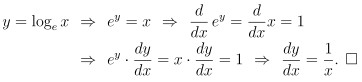
那式 (3) 和式 (1) 怎麼互通呢? 這是高等微積分裡一個很重要的定理:
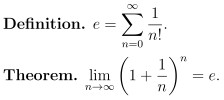
(Principles of Mathematical Analysis, 3th, Walter Rudin)
我們來看看這個證明: (下面的證明有一點瑕疵 這個後面再來解釋)
我們考慮下面兩個數列
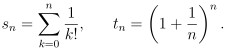
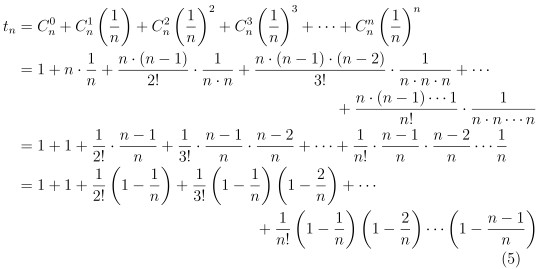
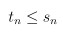
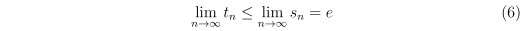
故當 n 取得比 m 大時 由式 (5) 可以推得
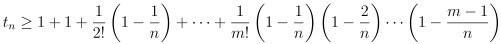
故兩邊同時對 n 取極限 (m 我們固定不動) 就會有
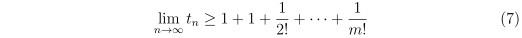
即 "數列 {tn} 的極限比 {sm} 裡的「每一項」都還要大 (因為 m 是隨意選的一個數)"
因此 即使我們對 {sm} 取極限 其極限還是會比 {tn} 的極限小
所以我們得到
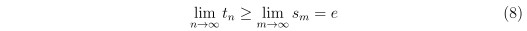
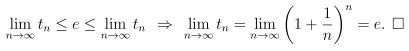
簡單講一下上面證明的瑕疵
但因為會用到高等微積分的東西 所以如果沒有想要深入追究的話 這一段是可以跳過的
上面證明有一個很嚴重的問題 在式 (6) 和式 (7) 的地方
以式 (6) 來說 因為 {tn} 每一項都比 {sn} 小 所以我們說 {tn} 的極限比 {sn} 小
但一個重要的問題是 如果 {tn} 本身不收斂 就完全沒有式 (6) 的關係了!!
所以 正確的說法應該是 limsup tn 而不是 lim tn
同樣的理由 式 (7) 應該要改為 liminf tn 才是正確的
因此 最後得到的是
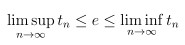
根據兩者的定義 我可以同時得到 "數列 {tn} 收斂" 而且 "其極限值為共同值 e"
至於 什麼是 limsup 跟 liminf ?
這就容我不在這裡多說了 要不然會寫不完啊~~~
後記:
從開始想寫這一篇文章 到 今天真的寫完 花了將近 1 個半月
其實 上面那些證明對我來說都很容易找得到且容易看得懂
但想到要寫得讓大部份的人可以看得懂 這真的讓我傷透腦筋
此外 再寫上篇的時候 一邊寫才一邊發現
有不少東西 我只是有 "印象" 但從來沒有深究過
因此把那些資料翻出來重讀了好幾次 才敢把他寫出來
再加上工作的關係 就只能每個週末挪一點時間出來寫
這下篇就是這樣接力寫了四個星期才完成
很辛苦 但很有成就感
尤其是看到上篇一個月就將近 100 人點閱
我相信這樣的文章 對某些人是有幫助的
這樣 我就開心了 ^^
參考資料:
全站熱搜


 留言列表
留言列表


