某廠商委託民調機構在甲、乙兩地調查聽過某項產品的居民佔當地居民之百分比 (以下簡稱為「知名度」)。結果如下:在 95% 信心水準之下,該產品在甲、乙兩地的知名度之信賴區間分別為 [ 0.50 , 0.58 ] 、 [ 0.08 , 0.16 ] 。試問下列哪些選項是正確的?
(1) 甲地本次的參訪者中, 54% 的人聽過該產品
(2) 此次民調在乙地的參訪人數少於在甲地的參訪人數
(3) 此次調查結果可解讀為:甲地全體居民中有一半以上的人聽過該產品的機率大於 95%
(4) 若在乙地以同樣方式進行多次民調,所得知名度有 95% 的機會落在區間 [ 0.08 , 0.16 ]
(5) 經密集廣告宣傳後,在乙地再次進行民調,並增加參訪人數達原人數的四倍,則在 95% 信心水準之下該產品的知名度之信賴區間寬度會減半 (即 0.04 )
==============================
這是今年大學學測數學科多選題第 9 題
考的是「信賴區間」這個新編入高中教材的觀念
雖然它出現在今年的考試題目中 這是大家預料中的事 而且相信一定會出現
可是這題的難度 可說是遠遠超出大家的預期 - 太難啦!!
我自己只對一個選項... 而且還搞不清楚自己是錯在哪裡...
今天趁著蔡蓉青老師 (我大學時的統計學老師) 難得七點多還在研究室 趕快去問個清楚
下面是我今天跟老師討論後的一些結論
選項(1) 「甲地本次的參訪者中,54% 的人聽過該產品」
首先 考題有提供 95% 信心水準下之信賴區間的公式:
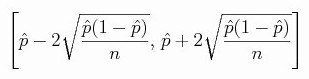
其中的 \hat{p} 是「這次調查」所得的知名度, n 是「這次調查」所調查的人數
為什麼要強調「這次調查」這四個字呢?
首先 我們不可能去問全部的人你知不知道這個東西 這樣費時又費力
因此 我們利用抽樣調查的方式 從全部的人中挑一部分的人出來接受調查
所以挑出來的人數 就是這裡的 n 即「這次調查」所調查的人數 而不是全部
在詢問過這 n 個人之後 我們可以計算出這 n 個人有聽過這個產品的比例 \hat{p}
但注意到 \hat{p} 是這 n 個人有聽過這個產品的比例 並不是所有人
很明顯的 「只問 n 個人所得到的比例」 幾乎不會跟 「問所有人所得到的比例」 一樣
因此 我在這裡強調 \hat{p} 是「這次調查」所得的知名度 並非是真正的狀況
這個問題問的就是 在甲地這 n 個人中有聽過該產品的比例 也就是 \hat{p}
因此從公式可以知道 \hat{p} = 0.50 和 0.58 的中間值 = 0.54
故這個選項是正確的
這麼簡單的題目 我是錯在哪裡呢?
我錯在我眼殘 沒有看到「本次的參訪者」這五個字
所以我以為題目是問 甲地「所有人」聽過這個產品的比例
如果是所有人的話 答案就是不知道 除非你把所有人都叫來問過才會知道
選項(2) 「此次民調在乙地的參訪人數少於在甲地的參訪人數」
簡單講 就是把兩地的 n 求出來比大小就是了
不過可以不用這麼麻煩 因為兩地信賴區間的寬度一樣 都是 0.08
也就是說兩者根號內部的值一樣 即 (0.54)(0.46) / 甲地人數 = (0.12)(0.88) / 乙地人數
稍微計算一下就可以知道 甲地人數是比較多的
那我是錯在哪裡?
我錯在有一個印象是 「當人數越多時 信賴區間會越窄」
因此我看到兩者的信賴區間是一樣的時候 很自然的以為兩者的人數一樣
「當人數越多時 信賴區間會越窄」這句話沒錯 錯是錯在這指的是對同一個調查而言
甲地和乙地的知名度是兩個完全不同的東西 怎麼可以用上面的理由來套
選項(3) 「此次調查結果可解讀為:甲地全體居民中有一半以上的人聽過該產品的機率大於 95%」
這個選項是錯的!
錯在哪裡? 錯在「甲地全體居民中有一半以上的人聽過該產品的『機率』」 錯在『機率』這個詞
在和老師討論的過程中 我用了三個階段來理解這個錯誤
第一個階段 我是用下面這個例子來理解的
「在還沒有擲骰子前 擲出 5 點的機率為 1/6;
但擲了骰子之後 就沒有機率可言 因為不是 100% (出現 5 點) 就是 0% (出現其他點)」
差別在於 前者是「臆測」 後者是「事實」
就很像我們在算期望值一樣 算出來大樂透的期望值是 28 塊多
但實際上會拿到的 不是「高額獎金」 就是「一毛都沒有」
「28 元」只是個臆測
同樣的 甲地的人
如果不是 「超過一半的人聽過該產品 (100%)」 就是 「少於一半的人聽過該產品 (0%)」
這是一個「事實」
只是我們不可能真的把甲地的人通通找來問 因此我們無法得知這個「事實」到底是 100% 還是 0%
第二個階段 我是用 「隨機變數」 這個統計學上的名詞來理解的
一樣用擲骰子的例子來解釋這個名詞
在還沒有擲骰子之前 對於等一下可能會擲出的數字 可以看成是一個變數 X
也就是說 X 可能是 1, 2, 3, 4, 5, 6
我們無法預測 X 會是多少 所以把 X 稱為「隨機變數」
但我們知道 這六個數字出現的機率都是 1/6 因此就會出現這個隨機變數的「機率分佈」
再舉個例子 例如我從全臺灣 18 歲男生中挑一個男生出來 他的身高為 X
則這個 X 也是一個隨機變數 (因為 X 可能的值太多了)
而我們把每一個可能身高的機率找出來 也就形成身高的機率分佈
我們常說的「常態分佈」指的就是某個隨機變數 X 的一種機率分佈
其他常見的還有 uniform, Poison... 等等
但是 一但我真的把骰子給骰出去 骰出 5 點, X 就等於 5, 骰出 3 點, X 就等於 3
他不再是一個變動的數 - 你總不能睜眼看著擲出的 5 點說 你剛剛擲出的點數有可能是 3 點喔
一樣地 當我真的抓一個男生出來 量出他的身高是 180 公分 那我們上面所假設的 X 就是 180
這個 X 就不再是「隨機變數」 而是一個「常數」
既然 X 不是「隨機變數」 當然就不會有「機率分佈」
因此我們不會去討論 X 的機率 因為根本沒有機率可以討論
同樣的 「甲地居民知道這個東西的比例」是一個「常數」
有 60% 的人知道這個東西 那我們的 X 就是 60%
只有 10% 的人知道 X 就是 10% 這是不會變的
既然是一個常數 當然就沒有機率分佈 也就不能去討論知道比例超過 50% 的機率為何
第三個階段 這是跟老師另外扯到的 所是所謂的「信心」
印象中 在看大考中心給的釋疑中 他說如果把原敘述改成
「甲地全體居民中有一半以上的人聽過該產品的『信心』為 95%」 這就對了
什麼是「信心」啊????
我用比較白話的方式來說
所謂的「95% 信心水準下之信賴區間」
意思是 當我用同樣的抽樣方式 對甲地的居民 做同樣的調查
每一次的調查 我都會得到一個屬於那次的知名度 \hat{p} 然後計算出一個這次的信賴區間
因為是隨機抽樣 所以每次得到的知名度應該不太可能會相同 因此每個信賴區間也都不太一樣
但我們可以確信
「大約有 95% 的信賴區間會包含真正的知名度 p」
也就是說 如果我做了 100 次這樣的調查 可能有些會涵蓋到真正的值 可能有些會偏掉
但是有涵蓋到真正知名度的信賴區間個數 他的期望值是 95 個
(我自己的解釋是 這樣做所得到的信賴區間 會有 95% 的機率涵蓋到真正的知名度)
(但老師用的詞很精準 因此有點害怕沒把意思寫完整 所以上面寫起來一整個給他有點囉唆 ^^|||)
不過 就如同第二個階段所講的 上面這些過程都是在還沒有去做調查之前所可以討論的
一但真的做了調查 真的把信賴區間「算」出來 例如這一題的 [ 0.50 , 0.58 ]
那真正的知名度 p 不是落在 0.50 與 0.58 之間 就是根本不在這個區間內
又是一個 100% 與 0% 的關係 所以根本沒有機率可言
但是 我們所找出來的 [ 0.50 , 0.58 ] 是用上面的想法所找出來的
因此 他會給我們一種「感覺」 就是真正知名度 p 會在這裡面的可能性很高
我對他的「信心」有 95% 之高
這樣講有點玄 如果是這樣說應該就會比較有感覺
如果現在你手上有兩個信賴區間
一個是 90% 信心水準下之信賴區間 一個是 95% 信心水準下之信賴區間
雖然可能兩者都包含到真正知名度 p 也可能只有一個 或更慘兩個都沒有包含到
但當你要從中選一個跟你的客戶講說這個商品在甲地的知名度時
95% 給你的「信心」會比 90 % 的還要多 因為你相信 95% 出錯的機會是比較小的
(雖然有可能他是剛好那 100 個中不包含 p 的那 5 個)
當然啦 不是因為他叫「95% 信心水準下之信賴區間」所以我們才說他的信心是 95%
正確的狀況是應該要反過來 因為有 95% 的信心他會包含正確值 所以才叫這個名稱
不過為什麼有 95% 的信心 這就要扯到很多其他的東西
這些我學過 但不是很熟 而且要扯很久 所以就用上面的方式來解釋吧 ^^
選項(4) 「若在乙地以同樣方式進行多次民調,所得知名度有 95% 的機會落在區間 [ 0.08 , 0.16 ]」
因為這個選項是我唯一答對的 也因此沒有問老師
然後呢 我現在仔細的讀了他的敘述
我反而有點說不出他是錯在哪裡 因為跟我原本認為的東西不太一樣
這個如果有機會問過老師 再來跟大家分享
選項(5) 「經密集廣告宣傳後,在乙地再次進行民調,並增加參訪人數達原人數的四倍,則在 95% 信心水準之下該產品的知名度之信賴區間寬度會減半 (即 0.04 )」
這個選項是錯誤的 而我直接講我是錯在哪裡好了
從公式來看 當人數增加為原本的四倍時 區間看起來好像真的會變成原本的 根號四分之一 也就是一半
但我忘了 上面的 \hat{p} 也會跟著變動
即使他沒有經過密集的廣告 每次民調所得到的結果 (\hat{p}) 也幾乎是不可能一樣
因此 每次所得到的信賴區間大小也幾乎都是不一樣的
但可以肯定的是 如果想要縮小信賴區間的大小 人數增加絕對是一個考慮的方向
簡言之
一個很重要的地方 就是「隨機變數」的觀念
或甚至應該這樣說
「機率論」「統計」(當然包括「信賴區間」)都是建立在「隨機變數」的概念上
但就現今的教材 二下先講了機率 統計(包含信賴區間) 三上才提隨機變數
當然 我們可以這樣說 在二下可以先用很直觀的方式來看機率與統計
(實際上 課本也是這樣編的)
如果這是編課綱的委員原本的期望 那像第三與第四個選項就不應該出現在學測
此外 第一次出現有關「信賴區間」的考題就把大家搞得團團轉
很擔心這個很生活化的觀念 對學生學起來卻變得很沉重
第一次就這麼恐怖了 那之後像指考或往後的考試 會不會更難?
能弄清楚還好 弄不請楚就只能開始咬文嚼字
如果題目這樣說 那就是「機率」的意思 如果這樣說就不是「機率」而是「信心」...
或甚至開始抄大學教科書或研究所考題來唸
那就真的可惜了這原本應該是很有趣的東西了
P.S. 因為統計真的不是我拿手的東西
所以如果您有發現上面所說的東西有錯誤 麻煩請一定要跟我說 我會盡快的做更正
以免錯誤的東西藉由網路到處傳遞 那就尷尬了
感謝
(1) 甲地本次的參訪者中, 54% 的人聽過該產品
(2) 此次民調在乙地的參訪人數少於在甲地的參訪人數
(3) 此次調查結果可解讀為:甲地全體居民中有一半以上的人聽過該產品的機率大於 95%
(4) 若在乙地以同樣方式進行多次民調,所得知名度有 95% 的機會落在區間 [ 0.08 , 0.16 ]
(5) 經密集廣告宣傳後,在乙地再次進行民調,並增加參訪人數達原人數的四倍,則在 95% 信心水準之下該產品的知名度之信賴區間寬度會減半 (即 0.04 )
==============================
這是今年大學學測數學科多選題第 9 題
考的是「信賴區間」這個新編入高中教材的觀念
雖然它出現在今年的考試題目中 這是大家預料中的事 而且相信一定會出現
可是這題的難度 可說是遠遠超出大家的預期 - 太難啦!!
我自己只對一個選項... 而且還搞不清楚自己是錯在哪裡...
今天趁著蔡蓉青老師 (我大學時的統計學老師) 難得七點多還在研究室 趕快去問個清楚
下面是我今天跟老師討論後的一些結論
選項(1) 「甲地本次的參訪者中,54% 的人聽過該產品」
首先 考題有提供 95% 信心水準下之信賴區間的公式:
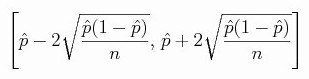
為什麼要強調「這次調查」這四個字呢?
首先 我們不可能去問全部的人你知不知道這個東西 這樣費時又費力
因此 我們利用抽樣調查的方式 從全部的人中挑一部分的人出來接受調查
所以挑出來的人數 就是這裡的 n 即「這次調查」所調查的人數 而不是全部
在詢問過這 n 個人之後 我們可以計算出這 n 個人有聽過這個產品的比例 \hat{p}
但注意到 \hat{p} 是這 n 個人有聽過這個產品的比例 並不是所有人
很明顯的 「只問 n 個人所得到的比例」 幾乎不會跟 「問所有人所得到的比例」 一樣
因此 我在這裡強調 \hat{p} 是「這次調查」所得的知名度 並非是真正的狀況
這個問題問的就是 在甲地這 n 個人中有聽過該產品的比例 也就是 \hat{p}
因此從公式可以知道 \hat{p} = 0.50 和 0.58 的中間值 = 0.54
故這個選項是正確的
這麼簡單的題目 我是錯在哪裡呢?
我錯在我眼殘 沒有看到「本次的參訪者」這五個字
所以我以為題目是問 甲地「所有人」聽過這個產品的比例
如果是所有人的話 答案就是不知道 除非你把所有人都叫來問過才會知道
選項(2) 「此次民調在乙地的參訪人數少於在甲地的參訪人數」
簡單講 就是把兩地的 n 求出來比大小就是了
不過可以不用這麼麻煩 因為兩地信賴區間的寬度一樣 都是 0.08
也就是說兩者根號內部的值一樣 即 (0.54)(0.46) / 甲地人數 = (0.12)(0.88) / 乙地人數
稍微計算一下就可以知道 甲地人數是比較多的
那我是錯在哪裡?
我錯在有一個印象是 「當人數越多時 信賴區間會越窄」
因此我看到兩者的信賴區間是一樣的時候 很自然的以為兩者的人數一樣
「當人數越多時 信賴區間會越窄」這句話沒錯 錯是錯在這指的是對同一個調查而言
甲地和乙地的知名度是兩個完全不同的東西 怎麼可以用上面的理由來套
選項(3) 「此次調查結果可解讀為:甲地全體居民中有一半以上的人聽過該產品的機率大於 95%」
這個選項是錯的!
錯在哪裡? 錯在「甲地全體居民中有一半以上的人聽過該產品的『機率』」 錯在『機率』這個詞
在和老師討論的過程中 我用了三個階段來理解這個錯誤
第一個階段 我是用下面這個例子來理解的
「在還沒有擲骰子前 擲出 5 點的機率為 1/6;
但擲了骰子之後 就沒有機率可言 因為不是 100% (出現 5 點) 就是 0% (出現其他點)」
差別在於 前者是「臆測」 後者是「事實」
就很像我們在算期望值一樣 算出來大樂透的期望值是 28 塊多
但實際上會拿到的 不是「高額獎金」 就是「一毛都沒有」
「28 元」只是個臆測
同樣的 甲地的人
如果不是 「超過一半的人聽過該產品 (100%)」 就是 「少於一半的人聽過該產品 (0%)」
這是一個「事實」
只是我們不可能真的把甲地的人通通找來問 因此我們無法得知這個「事實」到底是 100% 還是 0%
第二個階段 我是用 「隨機變數」 這個統計學上的名詞來理解的
一樣用擲骰子的例子來解釋這個名詞
在還沒有擲骰子之前 對於等一下可能會擲出的數字 可以看成是一個變數 X
也就是說 X 可能是 1, 2, 3, 4, 5, 6
我們無法預測 X 會是多少 所以把 X 稱為「隨機變數」
但我們知道 這六個數字出現的機率都是 1/6 因此就會出現這個隨機變數的「機率分佈」
再舉個例子 例如我從全臺灣 18 歲男生中挑一個男生出來 他的身高為 X
則這個 X 也是一個隨機變數 (因為 X 可能的值太多了)
而我們把每一個可能身高的機率找出來 也就形成身高的機率分佈
我們常說的「常態分佈」指的就是某個隨機變數 X 的一種機率分佈
其他常見的還有 uniform, Poison... 等等
但是 一但我真的把骰子給骰出去 骰出 5 點, X 就等於 5, 骰出 3 點, X 就等於 3
他不再是一個變動的數 - 你總不能睜眼看著擲出的 5 點說 你剛剛擲出的點數有可能是 3 點喔
一樣地 當我真的抓一個男生出來 量出他的身高是 180 公分 那我們上面所假設的 X 就是 180
這個 X 就不再是「隨機變數」 而是一個「常數」
既然 X 不是「隨機變數」 當然就不會有「機率分佈」
因此我們不會去討論 X 的機率 因為根本沒有機率可以討論
同樣的 「甲地居民知道這個東西的比例」是一個「常數」
有 60% 的人知道這個東西 那我們的 X 就是 60%
只有 10% 的人知道 X 就是 10% 這是不會變的
既然是一個常數 當然就沒有機率分佈 也就不能去討論知道比例超過 50% 的機率為何
第三個階段 這是跟老師另外扯到的 所是所謂的「信心」
印象中 在看大考中心給的釋疑中 他說如果把原敘述改成
「甲地全體居民中有一半以上的人聽過該產品的『信心』為 95%」 這就對了
什麼是「信心」啊????
我用比較白話的方式來說
所謂的「95% 信心水準下之信賴區間」
意思是 當我用同樣的抽樣方式 對甲地的居民 做同樣的調查
每一次的調查 我都會得到一個屬於那次的知名度 \hat{p} 然後計算出一個這次的信賴區間
因為是隨機抽樣 所以每次得到的知名度應該不太可能會相同 因此每個信賴區間也都不太一樣
但我們可以確信
「大約有 95% 的信賴區間會包含真正的知名度 p」
也就是說 如果我做了 100 次這樣的調查 可能有些會涵蓋到真正的值 可能有些會偏掉
但是有涵蓋到真正知名度的信賴區間個數 他的期望值是 95 個
(我自己的解釋是 這樣做所得到的信賴區間 會有 95% 的機率涵蓋到真正的知名度)
(但老師用的詞很精準 因此有點害怕沒把意思寫完整 所以上面寫起來一整個給他有點囉唆 ^^|||)
不過 就如同第二個階段所講的 上面這些過程都是在還沒有去做調查之前所可以討論的
一但真的做了調查 真的把信賴區間「算」出來 例如這一題的 [ 0.50 , 0.58 ]
那真正的知名度 p 不是落在 0.50 與 0.58 之間 就是根本不在這個區間內
又是一個 100% 與 0% 的關係 所以根本沒有機率可言
但是 我們所找出來的 [ 0.50 , 0.58 ] 是用上面的想法所找出來的
因此 他會給我們一種「感覺」 就是真正知名度 p 會在這裡面的可能性很高
我對他的「信心」有 95% 之高
這樣講有點玄 如果是這樣說應該就會比較有感覺
如果現在你手上有兩個信賴區間
一個是 90% 信心水準下之信賴區間 一個是 95% 信心水準下之信賴區間
雖然可能兩者都包含到真正知名度 p 也可能只有一個 或更慘兩個都沒有包含到
但當你要從中選一個跟你的客戶講說這個商品在甲地的知名度時
95% 給你的「信心」會比 90 % 的還要多 因為你相信 95% 出錯的機會是比較小的
(雖然有可能他是剛好那 100 個中不包含 p 的那 5 個)
當然啦 不是因為他叫「95% 信心水準下之信賴區間」所以我們才說他的信心是 95%
正確的狀況是應該要反過來 因為有 95% 的信心他會包含正確值 所以才叫這個名稱
不過為什麼有 95% 的信心 這就要扯到很多其他的東西
這些我學過 但不是很熟 而且要扯很久 所以就用上面的方式來解釋吧 ^^
選項(4) 「若在乙地以同樣方式進行多次民調,所得知名度有 95% 的機會落在區間 [ 0.08 , 0.16 ]」
因為這個選項是我唯一答對的 也因此沒有問老師
然後呢 我現在仔細的讀了他的敘述
我反而有點說不出他是錯在哪裡 因為跟我原本認為的東西不太一樣
這個如果有機會問過老師 再來跟大家分享
選項(5) 「經密集廣告宣傳後,在乙地再次進行民調,並增加參訪人數達原人數的四倍,則在 95% 信心水準之下該產品的知名度之信賴區間寬度會減半 (即 0.04 )」
這個選項是錯誤的 而我直接講我是錯在哪裡好了
從公式來看 當人數增加為原本的四倍時 區間看起來好像真的會變成原本的 根號四分之一 也就是一半
但我忘了 上面的 \hat{p} 也會跟著變動
即使他沒有經過密集的廣告 每次民調所得到的結果 (\hat{p}) 也幾乎是不可能一樣
因此 每次所得到的信賴區間大小也幾乎都是不一樣的
但可以肯定的是 如果想要縮小信賴區間的大小 人數增加絕對是一個考慮的方向
簡言之
一個很重要的地方 就是「隨機變數」的觀念
或甚至應該這樣說
「機率論」「統計」(當然包括「信賴區間」)都是建立在「隨機變數」的概念上
但就現今的教材 二下先講了機率 統計(包含信賴區間) 三上才提隨機變數
當然 我們可以這樣說 在二下可以先用很直觀的方式來看機率與統計
(實際上 課本也是這樣編的)
如果這是編課綱的委員原本的期望 那像第三與第四個選項就不應該出現在學測
此外 第一次出現有關「信賴區間」的考題就把大家搞得團團轉
很擔心這個很生活化的觀念 對學生學起來卻變得很沉重
第一次就這麼恐怖了 那之後像指考或往後的考試 會不會更難?
能弄清楚還好 弄不請楚就只能開始咬文嚼字
如果題目這樣說 那就是「機率」的意思 如果這樣說就不是「機率」而是「信心」...
或甚至開始抄大學教科書或研究所考題來唸
那就真的可惜了這原本應該是很有趣的東西了
P.S. 因為統計真的不是我拿手的東西
所以如果您有發現上面所說的東西有錯誤 麻煩請一定要跟我說 我會盡快的做更正
以免錯誤的東西藉由網路到處傳遞 那就尷尬了
感謝
全站熱搜


 留言列表
留言列表


