[題目] 利用尺規做圖法, 作過 A, B 兩點且與圓 O 相切的圓
今年帶系上大二的高等幾何 這是期中考的一個題目
說實話 我想了許久 還真的不知道要怎麼做
問過了老師 嗯 這是個有趣的做法 ^^
[作法]
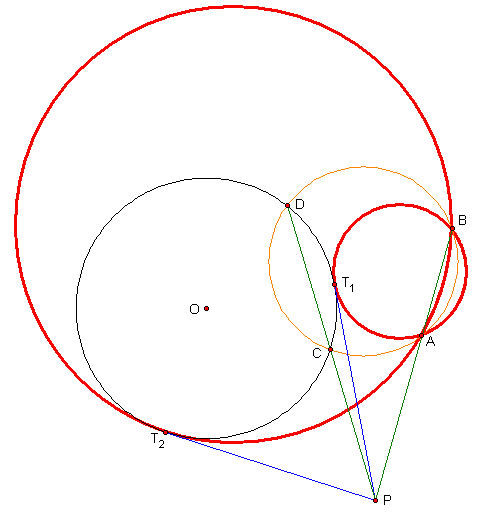
1. 對 A, B 兩點任做一個圓 (即橘色的圓) 使其與圓 O 交於兩點. 稱這兩點為 C 與 D.
2. 做 CD 延長線與 AB 延長線 (即綠色線), 令其交點為 P.
3. 做 P 點對圓 O 的切線 (即藍色線), 令兩切點分別為 T_1 與 T_2.
4. 做圓過點 A, B, T_1 與圓過 A, B, T_2 (即紅色圓), 這兩個圓即為所求.
[證明]
根據圓冪定理
由橘色圓知道 PA x PB = PC x PD ... (1)
因為 PT_1 為圓 O 的切線
由黑色圓知道 (PT_1)^2 = PC x PD ... (2)
由 (1) 與 (2) 知道 (PT_1)^2 = PC x PD = PA x PB
因此考慮圓 ABT_1, 則 PT_1 為這個圓的切線
因為 PT_1 同時為圓 O 與 圓 ABT_1 的切線 故這兩圓相切於 T_1
同理可得 圓 ABT_2 與圓 O 切於 T_2 點 Q.E.D.
我對圓冪定理很沒輒 或者應該這樣說 我不覺得圓冪定理重要或有用
現在 我得對他改觀囉 ^^
今年帶系上大二的高等幾何 這是期中考的一個題目
說實話 我想了許久 還真的不知道要怎麼做
問過了老師 嗯 這是個有趣的做法 ^^

[作法]
1. 對 A, B 兩點任做一個圓 (即橘色的圓) 使其與圓 O 交於兩點. 稱這兩點為 C 與 D.
2. 做 CD 延長線與 AB 延長線 (即綠色線), 令其交點為 P.
3. 做 P 點對圓 O 的切線 (即藍色線), 令兩切點分別為 T_1 與 T_2.
4. 做圓過點 A, B, T_1 與圓過 A, B, T_2 (即紅色圓), 這兩個圓即為所求.
[證明]
根據圓冪定理
由橘色圓知道 PA x PB = PC x PD ... (1)
因為 PT_1 為圓 O 的切線
由黑色圓知道 (PT_1)^2 = PC x PD ... (2)
由 (1) 與 (2) 知道 (PT_1)^2 = PC x PD = PA x PB
因此考慮圓 ABT_1, 則 PT_1 為這個圓的切線
因為 PT_1 同時為圓 O 與 圓 ABT_1 的切線 故這兩圓相切於 T_1
同理可得 圓 ABT_2 與圓 O 切於 T_2 點 Q.E.D.
我對圓冪定理很沒輒 或者應該這樣說 我不覺得圓冪定理重要或有用
現在 我得對他改觀囉 ^^
全站熱搜


 留言列表
留言列表


